Un asse senza massa ha una estremità attaccata al centro di una ruota (un disco di massa m e raggio r) e l'altra attaccata ad un pivot fissato al suolo.
La ruota rotola senza strisciare sul suolo con l'asse che forma un angolo costante

con l'orizzontale. Il punto di contatto della ruota con il suolo descrive una circonferenza con frequenza
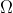
.
a) Dimostrare che
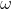
(frequenza di rotazione della ruota attorno al suo centro) punta verso destra con componente orizzontale pari a

b) Dimostrare che la forza normale N fra suolo e ruota è
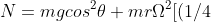 cos\theta sen^2 \theta + (3/2) cos^3 \theta])
(Edit con hints ) Si tratta di un problema tratto da
Introduction to Classical Mechanics di David Morin. Rispetto ad a) tenere conto della condizione di rotolamento ruota/suolo. Il quesito b) è più complicato: bisogna considerare le componenti di
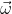
ovvero

e riportarle quindi sugli assi cartesiani

con origine nel pivot ma direzioni da determinare. Si deve trovare il momento angolare

dove

sono i momenti di inerzia della ruota rispetto a

e poi la sua componente orizzontale.....
