Pagina 1 di 3
317. Spira in campo magnetico
Inviato: 2 set 2023, 9:56
da Tarapìa Tapioco
Una spira circolare, fatta di un sottile filo conduttivo di raggio

, resistività
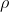
e densità di massa
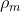
e posta lungo un piano orizzontale, cade da grande altezza in un campo magnetico avente una componente verticale che varia con

seguendo la legge
 = B_0 (1+ \alpha z))
. La spira, di diametro
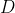
, durante la caduta mantiene l'orientazione orizzontale e un campo uniforme lungo le direzioni
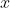
e
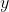
. Trascurando l'attrito dell'aria, calcolare la velocità finale di caduta della spira.
Re: 317. Spira in campo magnetico
Inviato: 2 set 2023, 11:15
da Physicsguy51
Let $\vec{n}$ be the normal to the plane of the ring, then the flux created by the vertical component of the magnetic field is $\Phi=B S=B_0(1+\alpha z) S$, where $S=\frac{\pi d^2}{4}$ - the area of the EMF induction that occurs in the ring,
$$
\mathcal{E}_i=-\Phi^{\prime}(t)=-\left(B_0(1+\alpha z) S\right)^{\prime}=-B_0 S \alpha z^{\prime}(t) \text {.}
$$
The derivative $z^{\prime}(t)=-v_z$ is the projection of the ring velocity onto the $z$ axis. Thus, $\mathcal{E}_i=-B_0 S \alpha\left(-v_z\right)$. Since the ring velocity is directed against the $z$ axis, then $v_z=-v$, where $v$ is the magnitude of the ring velocity and $\mathcal{E}_i=B_0 S \alpha \nu$. An induced current $I=\frac{\mathcal{E}_i}{R}=\frac{B_0 S \alpha v}{R}$ flows through the ring. As a result, an amount of heat $Q=I^2 R \Delta t$ is released in the ring over a period of time $\Delta t$
At a height of $z_1$, the ring has mechanical energy $W_1=m g z_1+\frac{m v^2}{2}$, at a height of $z_2-W_2=m g z_2+\frac{m v^2}{2}$ ( $v= $ const, i.e. the speed of the ring does not change). According to the law of conservation of energy $W_1=W_2+Q \Rightarrow m g z_1=m g z_2+I^2 R \Delta t \Rightarrow m g\left(z_1 z_2\right)=\left(\frac{B_0 S \alpha v}{R}\right )^2 R \Delta t \Rightarrow m g\left(z_1-z_2\right)\left(^*\right) \\ =\frac{\left(B_0 S \alpha v\right)}{R} \Delta t$
The difference $\left(z_1-z_2\right)$ is the distance covered by the ring during uniform motion, therefore $z_1-z_2=v \Delta t$, and equation will take the form:
$$
m g v \Delta t=\frac{\left(B_0 S \alpha v\right)^2}{R} \Delta t=\Rightarrow m g=\frac{\left(B_0 S \alpha\right)^2 v}{R} \Rightarrow v=\frac{m g R}{\left(B_0 S \alpha\right)^2}=\frac{16 m g R}{\left(B_0 \pi d^2 \alpha\right)^2}
$$
where $m$ is mass of loop and $d$ is its diameter.
Re: 317. Spira in campo magnetico
Inviato: 2 set 2023, 11:25
da Tarapìa Tapioco
Could you write the process using the LaTex tool on the Forum so that the language of the message is more understandable and readable? Also, I have modified the prompt, so you need to write the final result according to the data provided by the text. Sorry for the mistake.
P.S. Mass
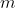
is not a datum given by the problem, but must be written as a function of what the exercise delivers.
Re: 317. Spira in campo magnetico
Inviato: 2 set 2023, 17:39
da Physicsguy51
Ok.
Let
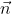
be the normal to the plane of the ring, then the flux created by the vertical component of the magnetic field is
 S)
, where
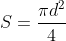
- the area of the EMF induction that occurs in the ring,
=-\left(B_0(1+\alpha z) S\right)^{\prime}=-B_0 S \alpha z^{\prime}(t) \text {.}
)
The derivative
=-v_z)
is the projection of the ring velocity onto the

axis. Thus,
)
. Since the ring velocity is directed against the

axis, then
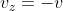
, where

is the magnitude of the ring velocity and

. An induced current
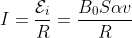
flows through the ring. As a result, an amount of heat
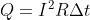
is released in the ring over a period of time
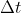
At a height of
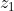
, the ring has mechanical energy
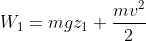
, at a height of
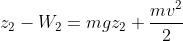
(

= const, i.e. the speed of the ring does not change). According to the law of conservation of energy
=\left(\frac{B_0 S \alpha v}{R}\right )^2 R \Delta t \Rightarrow m g\left(z_1-z_2\right)\left(^*\right) \\ =\frac{\left(B_0 S \alpha v\right)}{R} \Delta t)
The difference
)
is the distance covered by the ring during uniform motion, therefore
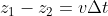
, and equation will take the form:
^2}{R} \Delta t=\Rightarrow m g=\frac{\left(B_0 S \alpha\right)^2 v}{R} \Rightarrow v=\frac{m g R}{\left(B_0 S \alpha\right)^2}=\frac{16 m g R}{\left(B_0 \pi d^2 \alpha\right)^2}
)
where
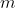
is mass of loop and
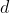
is its diameter. I know that we were given mass density and radius but in my answer you can just substitute
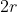
for diameter and
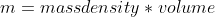
.
Re: 317. Spira in campo magnetico
Inviato: 2 set 2023, 17:44
da Physicsguy51
Hence final answer will be:
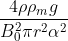
Re: 317. Spira in campo magnetico
Inviato: 2 set 2023, 17:50
da Physicsguy51
i made a calculation error.
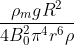
Re: 317. Spira in campo magnetico
Inviato: 2 set 2023, 18:32
da Tarapìa Tapioco
The final result is incorrect. Your first result is very very close to the official solution. But, again, you have to write it as a function of only the data provided by the text of the problem. Not only
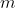
but also
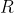
is a quantity not shown in the text.
Re: 317. Spira in campo magnetico
Inviato: 3 set 2023, 0:09
da Physicsguy51
Ok, this is what I am getting:
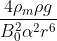
Re: 317. Spira in campo magnetico
Inviato: 3 set 2023, 0:16
da Tarapìa Tapioco
No, unfortunately, this is not the correct solution. Most likely, the error is due to your confusion between the diameter
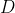
of the loop

which, therefore, has radius
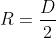
)
and the diameter
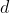
of the thin conducting wire

which, therefore, has radius
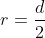
)
.
Re: 317. Spira in campo magnetico
Inviato: 3 set 2023, 0:25
da Physicsguy51
Oh, it seems like I neglected one of the two.. I assumed the loop to be of radius r...and directly conserved energy
 , resistività
, resistività 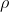 e densità di massa
e densità di massa 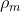 e posta lungo un piano orizzontale, cade da grande altezza in un campo magnetico avente una componente verticale che varia con
e posta lungo un piano orizzontale, cade da grande altezza in un campo magnetico avente una componente verticale che varia con  seguendo la legge
seguendo la legge  = B_0 (1+ \alpha z)) . La spira, di diametro
. La spira, di diametro 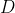 , durante la caduta mantiene l'orientazione orizzontale e un campo uniforme lungo le direzioni
, durante la caduta mantiene l'orientazione orizzontale e un campo uniforme lungo le direzioni 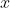 e
e 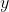 . Trascurando l'attrito dell'aria, calcolare la velocità finale di caduta della spira.
. Trascurando l'attrito dell'aria, calcolare la velocità finale di caduta della spira.