321. Torre infinita di cilindri

[Tarapìa Tapioco]

solo dopo di pensare a n generico, che è piuttosto difficile.

Non necessariamente. La difficoltà del caso in esame dipende soltanto da quale strada si scelga di prendere: una più lunga e classicamente formale, l'altra più breve e leggermente "truccosa".

[mantanp]

Penso di avere una difficoltà di fondo nel capire il caso più banale, ovvero n=1...
Ecco quello che ho pensato: sicuramente i cilindri accelerano a sinistra a causa della forza d'attrito e inoltre l'accelerazione del centro di massa del sistema corrisponde all'accelerazione dei due cilindri, essendo l'asse priva di massa. Ma quindi, non essendoci forze esterne che agiscono orizzontalmente sul sistema (gli attriti sono delle forze di interazione), l'accelerazione del centro di massa dovrebbe essere nulla rispetto al laboratorio, ovvero i due cilindri si muovono con accelerazione verso sinistra il che mi pare un po' strano.

[Pigkappa]

Non è vero che non ci sono forze esterne. Per mantenere l'asse in moto con accelerazione ed i cilindri in moto con l'accelerazione che bisogna trovare, qualcuno sta tirando l'asse.

Che l'accelerazione dei cilindri sia verso sinistra non è scontato... Combinando traslazione e rotazione si possono ottenere risultati inaspettati. Io non sapevo in che direzione si sarebbero mossi i cilindri finché non ho fatto i conti.

[mantanp]

Penso di non essere in grado di risolverlo, aspetto che qualche buon'anima scriva la soluzione o dia dei consigli per cominciare!

[Pigkappa]

Allego una immagine qua sotto. Nel cilindro a sinistra mostro la velocità lineare del CDM e quella angolare attorno al CDM, e 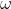rispettivamente. Nel cilindro a destra mostro le accelerazioni 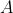e 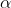e la forza di attrito .

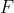Equazione 1: scrivere la legge fisica che collega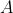 ed

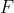
Equazione 2: scrivere la legge fisica che collega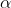 ed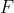

Equazione 3: scrivere il vincolo geometrico che soddisfa la condizione del testo per cui "i cilindri non strisciano rispetto alle assi"

Riesci a concludere da qui?

[mantanp]

Allora, con queste indicazioni io ricaverei queste tre equazioni:


Risolvendo il sistema, ottengo che , che potrebbe aver senso visto che significa che i cilindri ruotano verso sinistra, come avevamo detto! Magari qualcuno mi dia la conferma che abbia scritto equazioni giuste. Ora resta da pensare al caso

[Pigkappa]

Questa non mi convince. Attenzione ai segni...

[mantanp]

Io pensavo di imporre che il cilindro rotola rispetto alla trave che sta accelerando, quindi l'accelerazione "relativa" sarebbe . Cos'è che non va dei segni?

[Pigkappa]

Io lo farei così. La velocità di quel punto è . Nota bene che per come ho disegnato 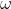, velocità angolare positiva lo fa ruotare verso destra, la stessa direzione di positiva. Affinché la accelerazione sia la stessa che l'asse, quindi .

Volendolo fare nel sistema di riferimento dell'asse, come fai tu, direi che la accelerazione di quel punto è e si deve imporre che questo sia zero.

In pratica, stai sbagliando a usare il segno di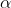 . Nell'equazione 2 hai usato il segno di 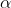e quindi nella 3 devi usarlo in modo concordante a quanto hai già fatto. Se io avessi disegnato 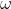nel verso opposto, sarebbe stata giusta la tua equazione 3 ma sbagliata la 2.

[mantanp]

Cambiando la terza equazione come suggerito, otterrei che . Ma non dovevano muoversi verso sinistra sti cilindri? Oppure me lo sono sognato io? Per quanto riguarda il caso con 4 cilindri, è giusto pensare che la forza d'attrito tra il cilindro ed il piano in alto abbia verso opposto a quello in basso (per permetterne il rotolamento)?