SNS n.1 2024
-
Marco Balsamo
- Messaggi: 8
- Iscritto il: 16 gen 2024, 19:37
SNS n.1 2024
Due oggetti di piccole dimensioni A e B, ciascuno con carica elettrica totale nulla, interagiscono tra loro elettrostaticamente con una forza attrattiva che dipende dalla distanza come  (dove n è un intero positivo). L’oggetto A è appeso a un punto fisso tramite un lungo filo inestensibile di massa trascurabile e lunghezza ℓ = 150 cm. Se si avvicina B ad A mantenendo entrambi alla stessa quota, A sposta la propria posizione di equilibrio dalla verticale. Quando la distanza tra i due oggetti scende sotto un certo valore, tuttavia, A si precipita spontaneamente verso B, rimanendovi attacato. Grazie a un righello disposto orizzontalmente sotto l’apparato, con lo zero sulla verticale del punto di sospensione, otto gruppi indipendenti di studenti/esse misurano i valori delle coordinate
(dove n è un intero positivo). L’oggetto A è appeso a un punto fisso tramite un lungo filo inestensibile di massa trascurabile e lunghezza ℓ = 150 cm. Se si avvicina B ad A mantenendo entrambi alla stessa quota, A sposta la propria posizione di equilibrio dalla verticale. Quando la distanza tra i due oggetti scende sotto un certo valore, tuttavia, A si precipita spontaneamente verso B, rimanendovi attacato. Grazie a un righello disposto orizzontalmente sotto l’apparato, con lo zero sulla verticale del punto di sospensione, otto gruppi indipendenti di studenti/esse misurano i valori delle coordinate 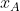 e
e 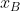 degli oggetti al momento in cui accade quanto descritto. Stimare il valore di n usando i dati riportati nella tabella, possibilmente discutendo le incertezze sperimentali (tabella:"https://i.ibb.co/ckXCCtZ/tabella.png"; immagine apparato: "https://i.ibb.co/F7Ygmz6/Fig-1.png").
degli oggetti al momento in cui accade quanto descritto. Stimare il valore di n usando i dati riportati nella tabella, possibilmente discutendo le incertezze sperimentali (tabella:"https://i.ibb.co/ckXCCtZ/tabella.png"; immagine apparato: "https://i.ibb.co/F7Ygmz6/Fig-1.png").
Re: SNS n.1 2024
Ho sintetizzato i conti ma se valesse la pena sono disposto ovviamente a esplicitarli...
Dalle misure effettuate risulta agevolmente che il valor medio di x risulta che dà luogo ad un'incertezza quadratica media
che dà luogo ad un'incertezza quadratica media^2 }{ n-1} } =\sqrt{ 0,1742}=0,42) di modo che la misura di x può essere espressa come il valor medio più o meno questa incertezza cioè
di modo che la misura di x può essere espressa come il valor medio più o meno questa incertezza cioè  . A questo punto mi ero posto il problema della conseguenza sulla forza F di attrazione che al momento dell'impatto deve essere la stessa ma che viene misurata diversamente dagli studenti e che contiene l'esponente -n. Infatti essa è proporzionale a
. A questo punto mi ero posto il problema della conseguenza sulla forza F di attrazione che al momento dell'impatto deve essere la stessa ma che viene misurata diversamente dagli studenti e che contiene l'esponente -n. Infatti essa è proporzionale a ovvero seguendo lo stesso ragionamento essendo
ovvero seguendo lo stesso ragionamento essendo  fornirebbe un'incertezza quadratica media su F pari a
fornirebbe un'incertezza quadratica media su F pari a ^n }}) . A questo punto non so andare avanti cioè valutare n in modo che questa incertezza sia minima? Sia massima? Mi pare una funzione monotonicamente decrescente che ovviamente si annulla per n tendente a infinito...
. A questo punto non so andare avanti cioè valutare n in modo che questa incertezza sia minima? Sia massima? Mi pare una funzione monotonicamente decrescente che ovviamente si annulla per n tendente a infinito... 

 Help,help dove sbaglio?
Help,help dove sbaglio?
Dalle misure effettuate risulta agevolmente che il valor medio di x risulta
Re: SNS n.1 2024
Ci ho provato stasera ma non ho una buona soluzione. Scrivo qua quel che ho pensato.
Il testo non mi è molto chiaro; non sono del sicuro che gli oggetti A e B siano gli stessi in tutti gli otto casi, né capisco se l'attrazione istantanea fortissima tra A e B avviene perché il filo si rompe o perché la relazione^{-n}) smette di funzionare a una certa distanza, o forse perché gli studenti non riescono a reggere B e lo lasciano andare.
smette di funzionare a una certa distanza, o forse perché gli studenti non riescono a reggere B e lo lasciano andare.
Per risolvere, assumo che nelle posizioni indicate in tabella i due oggetti siano in equilibrio. Non cerco di spiegare perché non lo sono appena diminuisce da quel valore, perché sinceramente non l'ho capito.
diminuisce da quel valore, perché sinceramente non l'ho capito.
Sia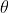 l'angolo con la verticale,
l'angolo con la verticale, 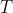 la tensione del filo,
la tensione del filo, 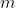 la massa di A,
la massa di A,  . Equazioni dell'equilibrio:
. Equazioni dell'equilibrio:

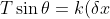^{-n})
Usando , da questa ricavando poi
, da questa ricavando poi 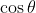 , e dividendo tra le due equazioni per eliminare
, e dividendo tra le due equazioni per eliminare 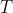 si trova:
si trova:
^n}{\sqrt{1 - (x_A / l)^2}} = \frac{kl}{m g})
I termini a destra sono sempre gli stessi, ma non conosciamo che non sono dati. Possiamo cercare il miglior valore di
che non sono dati. Possiamo cercare il miglior valore di 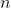 per cui l'espressione di sinistra
per cui l'espressione di sinistra ^n) è costante.
è costante.
Rimaneggiando, un altro modo di scrivere l'equazione sopra è:
^2}}} = C - n \ln{(\delta x)})
Dove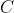 è una costante. Definisco
è una costante. Definisco ^2}}}) e
e }) e faccio il fit di
e faccio il fit di  rispetto ad una intercetta ed x. L'intercetta sarà la costante
rispetto ad una intercetta ed x. L'intercetta sarà la costante 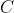 e la pendenza sarà
e la pendenza sarà 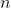 .
.
Il problema è che mettendo in un grafico, si vede che non si dispongono assolutamente su una retta. Anche solo facendo il plot di
in un grafico, si vede che non si dispongono assolutamente su una retta. Anche solo facendo il plot di  e
e  si nota che i punti sembrano messi a caso. Mostro i due grafici qua sotto.
si nota che i punti sembrano messi a caso. Mostro i due grafici qua sotto.
C'è qualcosa di fondamentale che non ho capito nel senso del problema. Se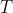 resiste fino all'infinito e i corpi sono avvicinati con estrema delicatezza e l'equazione della forza vale per ogni
resiste fino all'infinito e i corpi sono avvicinati con estrema delicatezza e l'equazione della forza vale per ogni  , mi verrebbe da pensare che si possa far arrivare il filo fino quasi ad arrivare in posizione verticale, ma devo sbagliarmi. Inoltre se B rimane fermo e A all'improvviso va ad attaccarsi, il filo si deve rompere per forza perché sennò A è vincolato ad una circonferenza e non riesce ad arrivare a B.
, mi verrebbe da pensare che si possa far arrivare il filo fino quasi ad arrivare in posizione verticale, ma devo sbagliarmi. Inoltre se B rimane fermo e A all'improvviso va ad attaccarsi, il filo si deve rompere per forza perché sennò A è vincolato ad una circonferenza e non riesce ad arrivare a B.

Il testo non mi è molto chiaro; non sono del sicuro che gli oggetti A e B siano gli stessi in tutti gli otto casi, né capisco se l'attrazione istantanea fortissima tra A e B avviene perché il filo si rompe o perché la relazione
Per risolvere, assumo che nelle posizioni indicate in tabella i due oggetti siano in equilibrio. Non cerco di spiegare perché non lo sono appena
Sia
Usando
I termini a destra sono sempre gli stessi, ma non conosciamo
Rimaneggiando, un altro modo di scrivere l'equazione sopra è:
Dove
Il problema è che mettendo
C'è qualcosa di fondamentale che non ho capito nel senso del problema. Se

"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: SNS n.1 2024
Io ho capito che 1) gli strumenti sono identici per tutti gli studenti (così mi sembra dalle stesse figure riportate da Marco) 2) la forza ^{-n }) smette di funzionare all'impatto BA , una forza di impatto che è UGUALE per tutti gli 8 studenti 3) essi danno tuttavia misure diverse di questa forza
smette di funzionare all'impatto BA , una forza di impatto che è UGUALE per tutti gli 8 studenti 3) essi danno tuttavia misure diverse di questa forza  stanti i loro diversi valori di
stanti i loro diversi valori di  (tabelle) che si esplicita nel valor medio
(tabelle) che si esplicita nel valor medio ; il valor medio può esprimersi come è noto come5,6
; il valor medio può esprimersi come è noto come5,6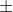 l'incertezza quadratica media su x ovvero
l'incertezza quadratica media su x ovvero  }{ n-1} }) 4) il mio risultato sarebbe x= 5,60
4) il mio risultato sarebbe x= 5,60 con denominatore n-1=7.
con denominatore n-1=7.
Con lo stesso procedimento ho calcolato l'incertezza media su . Dato che F=
. Dato che F= la sua incertezza sarà
la sua incertezza sarà ^n }) e la sua incertezza quadratica media sarà
e la sua incertezza quadratica media sarà }{{ 7(x-x_m)^n }) . E' a questo punto che mi fermo perchè non riesco a vedere il suo legame con n.
. E' a questo punto che mi fermo perchè non riesco a vedere il suo legame con n.
Il risultato che dai tu si fonda sulla costanza di^n) Questo secondo me è sbagliato perchè doveva essere
Questo secondo me è sbagliato perchè doveva essere \times \delta x^{ -n}) Comunque continueremo a pensarci chiedendo a tutti, a partire da Marco, di intervenire. Dopo tutto è stato assegnato a liceali anche se questi problemi sono famosi per essere oscuri a partire dal testo...
Comunque continueremo a pensarci chiedendo a tutti, a partire da Marco, di intervenire. Dopo tutto è stato assegnato a liceali anche se questi problemi sono famosi per essere oscuri a partire dal testo...
Con lo stesso procedimento ho calcolato l'incertezza media su
Il risultato che dai tu si fonda sulla costanza di
Re: SNS n.1 2024
Quello che io ho chiamato 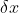 è
è 
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Marco Balsamo
- Messaggi: 8
- Iscritto il: 16 gen 2024, 19:37
Re: SNS n.1 2024
Secondo me il problema d'interpretazione risiede qui, quando dice:
. Per quanto ho capito io, al movimento di A, il corpo B si "riassesta" alla sua stessa ordinata; ovvero le misurazioni fatte dagli studenti sono intervallate a questi momenti di "assestamento". D'altronde il problema non ci dà che solo il riferimento nella direzione x.se si avvicina B ad A mantenendo entrambi alla stessa quota, A sposta la propria posizione di equilibrio dalla verticale
Re: SNS n.1 2024
Higgs ha scritto: ↑28 ott 2024, 18:16Io ho capito che 1) gli strumenti sono identici per tutti gli studenti (così mi sembra dalle stesse figure riportate da Marco) 2) la forzasmette di funzionare all'impatto BA , una forza di impatto che è UGUALE per tutti gli 8 studenti 3) essi danno tuttavia misure diverse di questa forza
stanti i loro diversi valori di
(tabelle) che si esplicita nel valor medio
; il valor medio può esprimersi come è noto come5,6
l'incertezza quadratica media su x ovvero
4) il mio risultato sarebbe x= 5,60
con denominatore n-1=7.
Con lo stesso procedimento ho calcolato l'incertezza media su. Dato che F=
la sua incertezza sarà
e la sua incertezza quadratica media sarà
. E' a questo punto che mi fermo perchè non riesco a vedere il suo legame con n.
Il risultato che dai tu si fonda sulla costanza diQuesto secondo me è sbagliato perchè doveva essere
Comunque continueremo a pensarci chiedendo a tutti, a partire da Marco, di intervenire. Dopo tutto è stato assegnato a liceali anche se questi problemi sono famosi per essere oscuri a partire dal testo...
Re: SNS n.1 2024
Ho visto la soluzione online da un'altra parte. Alla fine posterò il link per dare il merito all'autore, ma nel frattempo dò un suggerimento perché secondo me qua siamo bloccati, anche perché il testo è un po' oscuro.
Per una data posizione di B, il corpo A trova una posizione in cui è fermo e in equilibrio: gravità, tensione del filo e attrazione verso B si compensano.
Questo equilibrio è stabile?
Lascerei stare le otto misure per iniziare; farei la media delle misure e mi preoccuperei di trovare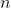 , che già è difficile. All'incertezza ci si pensa dopo.
, che già è difficile. All'incertezza ci si pensa dopo.
Per una data posizione di B, il corpo A trova una posizione in cui è fermo e in equilibrio: gravità, tensione del filo e attrazione verso B si compensano.
Questo equilibrio è stabile?
Lascerei stare le otto misure per iniziare; farei la media delle misure e mi preoccuperei di trovare
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Marco Balsamo
- Messaggi: 8
- Iscritto il: 16 gen 2024, 19:37
Re: SNS n.1 2024
Le forze in gioco sono tutte conservative, tranne la tensione. Ma in particolare il moto di A avviene lungo x dove la forza agente su A ha due termini: il primo è  che è la forza "di richiamo" del pendolo e considerando che
che è la forza "di richiamo" del pendolo e considerando che  possiamo scriverla come
possiamo scriverla come  con
con  che ha l'aspetto di una forza elastica con k costante equivalente. Mentre per quanto riguarda il termine di interazione elettrostatica
che ha l'aspetto di una forza elastica con k costante equivalente. Mentre per quanto riguarda il termine di interazione elettrostatica ^n}) .
.  è conservativa e si può dimostrare che anche
è conservativa e si può dimostrare che anche 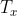 lo è. Allora vi possiamo associare i rispettivi potenziali e per la loro additività il potenziale associato alla risultante su A è la somma dei potenziali associati a
lo è. Allora vi possiamo associare i rispettivi potenziali e per la loro additività il potenziale associato alla risultante su A è la somma dei potenziali associati a 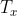 e
e  . In particolare: il potenziale associato a
. In particolare: il potenziale associato a 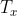 è quadratico [
è quadratico [ ], quello associato a
], quello associato a  è più complesso: è crescente e tende a zero a destra e a sinistra e diverge negativamente per
è più complesso: è crescente e tende a zero a destra e a sinistra e diverge negativamente per  . La funzione
. La funzione  = V_{T}+V_{F_{el}}) ha minimo in
ha minimo in 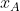 .
.
A questo punto @pigkappa chiedeva: , ma il testo ci dice che esiste un certo
, ma il testo ci dice che esiste un certo 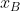 tale per cui B attrae A con una forza maggiore rispetto a quella di richiamo
tale per cui B attrae A con una forza maggiore rispetto a quella di richiamo 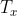 , cioé tutta la parte di grafico compresa tra
, cioé tutta la parte di grafico compresa tra ) tale che
tale che  con
con  estremo inferiore dell'intervallo "critico", cioè quello all'interno del quale per tutte le posizioni di B appartenenti allo stesso,
estremo inferiore dell'intervallo "critico", cioè quello all'interno del quale per tutte le posizioni di B appartenenti allo stesso,  . Ovviamente a noi interessa il valore minimo che assume
. Ovviamente a noi interessa il valore minimo che assume  , cioè
, cioè  . Dunque:
. Dunque: ^n}=0) e
e ^{n+1}}=0) . Mi sono arrestato, però, a questo punto: mi sembra che se noi mettiamo a sistema le due condizioni ci sia un dato in meno, sebbene non riesca a guardare altrove, forse c'è qualche espediente matematico, come posso rimediare? Non mi sembra che ci siano terze condizioni, poichè l'idea da cui ero partito è stata quella di semplificare la forma della funzione della forza su A facendo perno sulle due condizioni al contorno.
. Mi sono arrestato, però, a questo punto: mi sembra che se noi mettiamo a sistema le due condizioni ci sia un dato in meno, sebbene non riesca a guardare altrove, forse c'è qualche espediente matematico, come posso rimediare? Non mi sembra che ci siano terze condizioni, poichè l'idea da cui ero partito è stata quella di semplificare la forma della funzione della forza su A facendo perno sulle due condizioni al contorno.
A questo punto @pigkappa chiedeva:
Condizione necessaria ma non sufficiente per la stabilità della posizione di equilibrio è che
Ultima modifica di Marco Balsamo il 2 nov 2024, 0:13, modificato 3 volte in totale.
Re: SNS n.1 2024
Si può risolvere per  . Non serve calcolare
. Non serve calcolare  né
né 
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
