2) (Nel seguente problema tutte le coordinate sono da considerarsi in
Tiri al bersaglio
Tiri al bersaglio
1) Un drone parte da fermo nell'origine nel campo gravitazionale costante 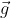 con accelerazione
con accelerazione  . Si intende lanciare un proiettile dal punto
. Si intende lanciare un proiettile dal punto ) per abbattere il drone. Qual è la velocità minima per raggiungere tale scopo?
per abbattere il drone. Qual è la velocità minima per raggiungere tale scopo?
2) (Nel seguente problema tutte le coordinate sono da considerarsi in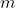 ). Dal punto
). Dal punto ) viene lanciata una pietra con velocità iniziale
viene lanciata una pietra con velocità iniziale  . Un uomo a terra in
. Un uomo a terra in ) vede che il lancio sta per avvenire e, valutando la pericolosità della pietra, decide di lanciare simultaneamente alla prima una seconda pietra con la minima velocità sufficiente per colpire la prima (e conseguentemente distruggerle entrambe). E' noto che il punto di collisione è (35, 12), trova le velocità
vede che il lancio sta per avvenire e, valutando la pericolosità della pietra, decide di lanciare simultaneamente alla prima una seconda pietra con la minima velocità sufficiente per colpire la prima (e conseguentemente distruggerle entrambe). E' noto che il punto di collisione è (35, 12), trova le velocità  e
e 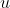 .
.
2) (Nel seguente problema tutte le coordinate sono da considerarsi in
Re: Tiri al bersaglio
Penso che se non dai qualche spunto di soluzione nessuno affronterà il problema 
 sono ormai oltre due settimane...
sono ormai oltre due settimane...
Re: Tiri al bersaglio
1) Io la vedo così. Le equazioni parametriche del drone sono 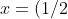gt^2 ; y= -(1/2)gt^2) e pertanto la traiettoria del drone è sul piano cartesiano y=-x bisettrice del quarto quadrante a partire dall'origine. La traiettoria del proiettile che supponiamo rettilinea e che parte da (-h,-h) forma un angolo
e pertanto la traiettoria del drone è sul piano cartesiano y=-x bisettrice del quarto quadrante a partire dall'origine. La traiettoria del proiettile che supponiamo rettilinea e che parte da (-h,-h) forma un angolo  con l'asse x che può variare fra +
con l'asse x che può variare fra + e
e 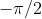 quando la traiettoria del proiettile è parallela a quella del drone cioè alla bisettrice del quarto quadrante. Le sue equazioni parametriche sono ora
quando la traiettoria del proiettile è parallela a quella del drone cioè alla bisettrice del quarto quadrante. Le sue equazioni parametriche sono ora  se v è la sua velocità. Quando il proiettile incontra il drone deve accadere la coincidenza delle loro coordinate e quindi
se v è la sua velocità. Quando il proiettile incontra il drone deve accadere la coincidenza delle loro coordinate e quindi gt^2 = -h+vt cos\alpha ; -(1/2)gt^2=-h+vt sen\alpha) ovvero semplificando
ovvero semplificando 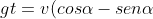) . Siccome il primo membro è un dato, v sarà minima quando la differenza
. Siccome il primo membro è un dato, v sarà minima quando la differenza  è massima ovvero quando
è massima ovvero quando 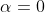 e la differenza vale 1. Insomma secondo questo ragionamento la traiettoria del proiettile dovrebbe essere parallela all'asse x. Il tempo di percorrenza del drone per arrivare all'impatto è ovviamente uguale a quello del proiettile.
e la differenza vale 1. Insomma secondo questo ragionamento la traiettoria del proiettile dovrebbe essere parallela all'asse x. Il tempo di percorrenza del drone per arrivare all'impatto è ovviamente uguale a quello del proiettile.
Sentito il giudizio su 1) vedrò il 2).
Sentito il giudizio su 1) vedrò il 2).
Re: Tiri al bersaglio
Mah, sinceramente non capisco perchè hai posto il problema Tiri al bersaglio...
Re: Tiri al bersaglio
Nonostante l'assenza di risposte provo a fare anche il secondo esercizio
2) Si può procedere così. Si calcolano facilmente le equazioni delle parabole percorse dal drone e dal proiettile conoscendo un punto e il vertice. Per ciascuna delle due si può calcolare le equazioni parametriche fisiche e dall'uguaglianza che deve verificarsi si calcolano v ed u.
La parabola del drone, partendo da (0,10) e avendo il vertice in (35,12), risulta
 = -(2/1225)x^2 + (28/245)x + 10) mentre
mentre = -(3/100)x^2+(21/10)x-(99/4)) Il vertice è lo stesso ed il tempo impiegato a raggiungerlo deve essere IDENTICO. Partendo dalle equazioni parametriche possiamo arrivare alle equazioni fisiche che devono coincidere con le precedenti.
Il vertice è lo stesso ed il tempo impiegato a raggiungerlo deve essere IDENTICO. Partendo dalle equazioni parametriche possiamo arrivare alle equazioni fisiche che devono coincidere con le precedenti.
Cominciamo con il drone. Le equazioni parametriche, non essendoci forza esterna lungo x, saranno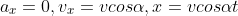 dove
dove  è l'angolo formato con l'asse x dalla tangente nel punto di partenza. Analogamente agendo la forza peso sulla massa
è l'angolo formato con l'asse x dalla tangente nel punto di partenza. Analogamente agendo la forza peso sulla massa 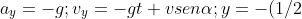gt^2+v sen\alpha t+10) . Questa equazione deve coincidere con quella cartesiana per cui
. Questa equazione deve coincidere con quella cartesiana per cui=(1/2)g(1/v^2cos^2\alpha)) . la
. la  da cui
da cui =(60281/245^2)) e si ottiene
e si ottiene 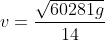
Analogamente si procede con il proiettile in cui l'equazione cartesiana della parabola descritta è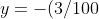x^2+ (21/10)x - 99/4) . Indicato con
. Indicato con 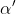 l'angolo formato dalla tangente alla partenza con l'asse x risulta
l'angolo formato dalla tangente alla partenza con l'asse x risulta  e dunque
e dunque  . L'equazione parametrica è ora
. L'equazione parametrica è ora g \frac{(x-15)^2 }{(u cos\alpha')^2 } + tang\alpha' (x-15) - 99/4) per cui uguagliando i primi addendi dell'equazione cartesiana e di quella parametrica si ottiene con facili calcoli
per cui uguagliando i primi addendi dell'equazione cartesiana e di quella parametrica si ottiene con facili calcoli

2) Si può procedere così. Si calcolano facilmente le equazioni delle parabole percorse dal drone e dal proiettile conoscendo un punto e il vertice. Per ciascuna delle due si può calcolare le equazioni parametriche fisiche e dall'uguaglianza che deve verificarsi si calcolano v ed u.
La parabola del drone, partendo da (0,10) e avendo il vertice in (35,12), risulta
Cominciamo con il drone. Le equazioni parametriche, non essendoci forza esterna lungo x, saranno
Analogamente si procede con il proiettile in cui l'equazione cartesiana della parabola descritta è
Re: Tiri al bersaglio
Mi scuso per la mia assenza dal forum per molto tempo, non vedendo inizialmente risposte al problema credevo fosse rimasto inconsiderato. In ogni caso chiarisco alcuni punti sul testo del problema. Il drone con i suoi motori mantiene la quota, quindi la sua accelerazione è unicamente
Re: Tiri al bersaglio
Per quanto riguarda questo sei sicuro dell'equazione della traiettoria, in particolare del fatto che il punto di collisione coincida con il vertice della parabola del drone (che è una pietra)? Inoltre guardando i tuoi risultati non sono corretti dimensionalmente. Come idea di soluzione prova a non considerarlo necessariamente nel sistema del laboratorio, in particolare se ne può trovare uno in cui le traiettorie hanno una forma "migliore".Higgs ha scritto: ↑19 giu 2025, 17:19Si calcolano facilmente le equazioni delle parabole percorse dal drone e dal proiettile conoscendo un punto e il vertice. Per ciascuna delle due si può calcolare le equazioni parametriche fisiche e dall'uguaglianza che deve verificarsi si calcolano v ed u.
La parabola del drone, partendo da (0,10) e avendo il vertice in (35,12), risulta
mentre
Il vertice è lo stesso ed il tempo impiegato a raggiungerlo deve essere IDENTICO. Partendo dalle equazioni parametriche possiamo arrivare alle equazioni fisiche che devono coincidere con le precedenti.
-
Mangogiallo26
- Messaggi: 6
- Iscritto il: 30 giu 2025, 20:17
Re: Tiri al bersaglio
Provo anch'io la soluzione del problema (per sdr intendo sistema di riferimento):
1) mettiamoci nel sdr uniformemente accelerato solidale con il drone. A questo punto sul sasso agisce un'accelerazione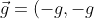) , la cui risultante è perciò un'accelerazione di
, la cui risultante è perciò un'accelerazione di  lungo la direzione della bisettrice del primo e terzo quadrante. La velocità minore con cui è possibile raggiungere il drone è quella per cui il sasso si ferma nell'origine, che risulta quindi
lungo la direzione della bisettrice del primo e terzo quadrante. La velocità minore con cui è possibile raggiungere il drone è quella per cui il sasso si ferma nell'origine, che risulta quindi


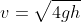
2)mettiamoci nel sdr in caduta libera. Ho che sui due sassi non agiscono forze e si muoveranno quindi di moto rettilineo uniforme, mentre il punto di contatto si muoverà secondo una legge del tipo
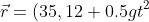)
Ad un dato istante t le due distanze del punto di contatto dai punti di partenza dei sassi sono:
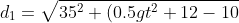^2}= vt)
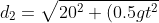^2}= ut)
Elevando al quadrato si possono ottenere
t^2+1129=0)

Dalle condizioni di esistenza del discriminante si possono ottenere le seguenti


Da cui risolvendole
^{0.25})
g })
Non ho ricontrollato i calcoli e ho qualche dubbio su come ho risolto le velocità nel secondo, però per il resto penso vada bene.
1) mettiamoci nel sdr uniformemente accelerato solidale con il drone. A questo punto sul sasso agisce un'accelerazione
2)mettiamoci nel sdr in caduta libera. Ho che sui due sassi non agiscono forze e si muoveranno quindi di moto rettilineo uniforme, mentre il punto di contatto si muoverà secondo una legge del tipo
Ad un dato istante t le due distanze del punto di contatto dai punti di partenza dei sassi sono:
Elevando al quadrato si possono ottenere
Dalle condizioni di esistenza del discriminante si possono ottenere le seguenti
Da cui risolvendole
Non ho ricontrollato i calcoli e ho qualche dubbio su come ho risolto le velocità nel secondo, però per il resto penso vada bene.
-
Mangogiallo26
- Messaggi: 6
- Iscritto il: 30 giu 2025, 20:17
Re: Tiri al bersaglio
Ho rivisto la soluzione del 2 punto e non mi convince per nulla. Vergognandomi di cosa ho fatto provo a rimediare:
Prendendo sempre il riferimento accelerato ho che se i sassi si incontrano in un tempo t le velocità risultano essere:



Risolvendole si ottengono le componenti da cui si ricavano i quadrati dei moduli delle velocità
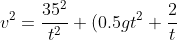^2= \frac{4516+g^2t^4}{4t^2}+ 2g )
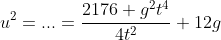
Facendo la derivata rispetto a t di u^2 (che tanto ha minimo nello stesso punto di u) e ponendola uguale a zero trovo il minimo
}{16 t^4})

Sostituendo questo tempo nelle equazioni di v e u si possono trovare le due velocità
Scusate se ho saltato un bel po’ di calcoli ma la stanchezza si fa sentire.
Prendendo sempre il riferimento accelerato ho che se i sassi si incontrano in un tempo t le velocità risultano essere:
Risolvendole si ottengono le componenti da cui si ricavano i quadrati dei moduli delle velocità
Facendo la derivata rispetto a t di u^2 (che tanto ha minimo nello stesso punto di u) e ponendola uguale a zero trovo il minimo
Sostituendo questo tempo nelle equazioni di v e u si possono trovare le due velocità
Scusate se ho saltato un bel po’ di calcoli ma la stanchezza si fa sentire.
Re: Tiri al bersaglio
Direi che la soluzione della prima parte funziona, molto beneMangogiallo26 ha scritto: ↑30 giu 2025, 20:42
1) mettiamoci nel sdr uniformemente accelerato solidale con il drone. A questo punto sul sasso agisce un'accelerazione, la cui risultante è perciò un'accelerazione di
lungo la direzione della bisettrice del primo e terzo quadrante. La velocità minore con cui è possibile raggiungere il drone è quella per cui il sasso si ferma nell'origine, che risulta quindi
