Nel mio post del 3 Dicembre stavo seguendo la tua notazione nella quale
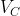
era positivo verso sinistra e le altre velocita' verso destra. Notazione legittima e che potrebbe essere utile perche' in generale ci aspettiamo che queste velocita' abbiano segni diversi.
Nel post del 10 Dicembre invece usavo la notazione che mi pare piu' naturale, in cui tutte le velocita' sono positive verso destra. Avrei dovuto segnalarlo per chiarezza, chiedo scusa.
In ogni caso cambia solo il segno di
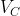
nella prima equazione e nei risultati finali, ma ovviamente

rimane sempre positivo essendo un quadrato, e nella tua equazione dell'energia non lo era.
Usando i miei risultati per

, scrivo:
 V_C})
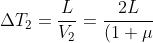 V_C})
Che a me darebbe:

Mi viene quindi diverso da te... Penso sia perche' nel post del 12 Dicembre, a differenza dei tuoi post precedenti, non usavi piu' le velocita' relative. Questo va bene e anche io sto facendo cosi', ma allora al denominatore di

devi fare attenzione e usare

invece di
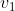
.
Il mio risultato ha senso?
Se

, la scatola esterna rimane praticamente ferma ovvero

e

, la particella ha sempre la stessa velocita' andando avanti e indietro, quindi ci aspettiamo di trovare

, che combacia con il risultato qua sopra.
Il tuo risultato invece da'

che mi sembra poco intuitivo. E se

trovi un rapporto negativo che e' a sua volta un po' strano.
Una spiegazione del perche' viene 1 potrebbe essere questa. Osserviamo lo stesso moto in un sistema di riferimento
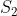
che si muove con velocita'
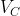
rispetto al sistema iniziale
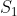
. Allora il moto e' simile a prima, ma abbiamo invertito quello che succede negli intervalli 1 e 2, e il segno della velocita': adesso nell'intervallo 1 la scatola e' ferma, nell'intervallo 2 si muove con velocita'

.
L'intervallo

e' lo stesso in entrambi i sistemi di riferimento, e nella relativita' galileiana cambiare sistema di riferimento inerziale non cambia i tempi, quindi:

, dove indico con

il valore di

misurato nel sistema
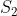
, e allo stesso modo uso la notazione

.
Pero' potremmo anche calcolare

risolvendo, nel sistema
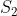
, il problema che avevamo risolto in
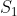
per calcolare

. Poiche' il problema e' identico a parte il segno delle velocita' (la lunghezza
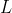
non cambia perche' non siamo in relativita'), troveremo

.
Mettendo insieme queste equazioni e' chiaro che

"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)

