321. Torre infinita di cilindri

[Pigkappa]

Giusto .

Mi sembra plausibile che si muovano verso destra. Nel caso estremo in cui non possono ruotare, ad esempio se fossero blocchi rettangolari invece che cilindri, la situazione sarebbe analoga ma con . Troveremmo e , diretto verso destra, che intuitivamente è corretto... Ma, come ho detto sopra, prima di fare il conto e trovare non ero sicuro.

Sulla generalizzazione per ora me ne sto zitto

[Higgs]

Nel tuo schema mi sembra che la rotazione faccia andare il cilindro indietro verso sinistra. Perchè F di attrito è diretta a destra in avanti e sembra favorire la rotazione indietro?

[Higgs]

Io la vedo così. La forza F di Pigkappa è quella che causa l'accelerazione a del cilindro rispetto al pavimento. Lo stesso Pigkappa la individuava come ragione del moto quando individuava la forza esterna agente e dunque mi sembra debba essere F=Ma. Ora come riconosceva anche Fidbg il 28/6 a questa accelerazione a deve essere tolta la rotazione verso sinistra del cdm. Questa rotazione con accelerazione deve soddisfare a da cui si ricava e quindi in definitiva . Osservo che, se va bene, è più semplice e aderente al testo del problema.

[Pigkappa]

Da dove viene questa?

[Higgs]

Ho pensato che siccome la forza F=Ma è applicata all'asse di rotazione e non al cdm, essa provoca la rotazione in senso opposto da parte di quest'ultimo con un momento negativo (opposto) del valore evidente MaR nella seconda legge di Newton sugli oggetti ruotanti. Quindi c'è traslazione della massa governata da F=Ma e rotazione sinistrorsa della stessa massa concentrata nel cdm governata dalla seconda legge di Newton sulle rotazioni . Risulta allora che l'accelerazione netta A=a/3 del cdm è proprio la differenza fra quella traslazionale a e quella rotazionale (2/3) a aventi versi opposti.

[Pigkappa]

Fatico a vedere la rotazione della massa concentrata nel CDM, sinceramente... Penso il tuo argomento si possa rendere più chiaro ma così com'è non l'ho capito in pieno.

Dato che siamo fermi da un po' posto la mia soluzione completa; è lunga e faticosa. Fibdg e Tarapia, se ne avete di migliori postatele

[Pigkappa]

Per semplificare le formule, poniamo e . Il momento di inerzia è .

Ci sono due cilindri per strato ma questo serve solo per evitare che le assi si inclinino. Basta considerare le forze agenti su una sola torre di cilindri.

Assegno numeri agli strati così che l'asse sotto a tutte le altre sia numerata come , con accelerazione è . L'asse più in alto sia . Nell'immagine qua sotto mostro la situazione del cilindro , che sente una forza dovuta all'asse sotto di lui, e del cilindro .

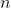
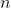
Il cilindro sente una forza ; per azione e reazione, esercita una forza opposta sull'asse sotto di lui. Ma l'asse è priva di massa, quindi la somma delle forze su di essa è nulla, quindi il cilindro deve esercitare una forza sull'asse e subire da sopra una forza .

In figura ho evidenziato l'accelerazione del CDM e la velocità angolare di rotazione . In realtà più che la velocità angolare ci interessa l'accelerazione angolare .

Cerchiamo equazioni ricorsive che mettano in relazione le variabili e quelle per .

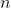
Usiamo le condizioni fisiche.

La seconda legge di Newton dà (1) .

La legge del momento della forza dà (2) .

Facendo la somma si ricava (3): .

Evidentemente la (3) deve valere anche se sostituiamo gli indici per il cilindro successivo ottenendo (4): .

Facendo la differenza tra (2) e (1): e usando la (4) qua dentro otteniamo la prima relazione ricorsiva che chiamo (5):

Ora usiamo le condizioni geometriche.

Il punto superiore del cilindro inferiore deve restare fermo rispetto all'asse di mezzo (6): .

Lo stesso dicasi per il punto inferiore del cilindro superiore (7): .

Mettendo insieme la (6) e la (7) otteniamo la seconda equazione ricorsiva (8):

Maneggiamo le relazioni ricorsive
Usando la (5) e la (8) ricaviamo e , equazioni (9) e (10):



Definiamo le condizioni al contorno
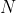
La condizione fisica sull'asse più in alto, che sente una sola forza è (11): .

La condizione geometrica per il punto inferiore dell'asse più in basso è (12): .

Contiamo le equazioni
Le incognite e sono . Le equazioni ricorsive (9) e (10) forniscono N equazioni ciascuna e le condizioni al contorno (11) e (12) sono le due equazioni mancanti. Abbiamo finito - possiamo ricavare tutte le incognite.

Per ottenere una risposta esplicita dobbiamo però fare alcuni passaggi.

Semplifichiamo le equazioni ricorsive
Trasformiamo le equazioni (9) e (10) in una forma più facile da usare. Se fossero nella forma sarebbe chiaro che avremmo , ma poiché ci sono due variabili che si mischiano tra loro, la nostra vita non è così semplice.

Allora cerchiamo una combinazione lineare di e tale che la formula ricorsiva sia del tipo .

Facendo un po' di lavoro (eufemismo!) ne troviamo due. Queste sono e . Le equazioni di ricorrenza le chiamo (13) e (14):


Si può verificare, sostituendo qua dentro i valori e dalla (9) e (10), che sono corrette.

Questo ci permette di saltare direttamente tra l'indice 0 ed N:



Usiamo le condizioni al contorno
Usiamo la (12) a sinistra e (11) a destra:


Dividiamo membro a membro e semplifichiamo i radicali. Ometto alcuni passaggi. Si ottiene la (15):


Facciamo il limite
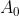
Si vede che per il termine di destra va all'infinito. Evidentemente, deve essere così anche a sinistra. Guardando il denominatore, questo ci dice che tende a . Problema risolto!

Risolviamo il caso N finito
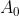
Già che ci siamo, possiamo ricavare in generale. Facendo il conto partendo dalla (15):


Il caso corrisponde ad avere un solo cilindro. In tal caso:



Che è il risultato di mantenp.

Il caso dà il risultato come sopra.

[mantanp]

Grazie mille per la soluzione dettagliata! Problema molto carino, forse più complicato dal punto di vista matematico che fisico ma comunque insegna molte cose sulla differenza tra rotolamento e scivolamento per esempio.

[Higgs]

Sicuramente mi sbaglio dato che il risultato è corretto ma componendo la 5) e la 8) non mi torna in funzione di perchè se addiziono scompare e se sottraggo scompare

[mantanp]

Se sommi non ottieni nulla, devi sostituire.
Dalla (8) ottieni che , quindi ora puoi prendere dalla (5) l'espressione e sostituirla ottenendo la (9):


Sostituendo questa espressione qua nella (5) ottieni poi la (10)!